副标题#e#    SolidWorks是当今造型、仿真方面最为流行的三维CAD软件，它具有基于特征进行参数化造型设计特点，模型各个特征的几何形状与尺寸大小用变量参数来表达，变量参数不仅可以是常数，也可以是某种代数式。如果定义某个特征的变量参数发生了改变，则模型的这个特征的几何形状或尺寸大小将随着参数的改变而改变，通过控制各种参数，即可以达到控制模型几何形体的目的。COSMOSMotion是SolidWorks自带的插件，和SolidWorks无缝对接，直接使用SolidWorks的数据库，对系统的运动学、动力学和静力学进行分析和仿真…。对于顶杆运动形式可用连续函数表达的凸轮轮廓曲线设计，可通过用SolidWorks构造基本的模型，在COSMOS Motion中输入凸轮和顶杆的运动约束函数表达式，然后模拟凸轮机构的运行状况，最终设计得到凸轮轮廓曲线。
   
    但在实际应用中，对顶杆的约束往往不能用函数来表示，只明确了几个位置的精确要求，其他位置没有精确的数值要求，把这种情况的凸轮轮廓曲线设计简称为离散点凸轮轮廓曲线设计。离散点凸轮轮廓曲线设计可通过用多项式等函数拟合各离散点，得到约束函数后再用前述的办法来设计。本文将具体研究利用COSMOS Motion自带样条函数自动实现离散点值拟合，模拟运行凸轮机构，生成凸轮轮廓曲线，并对凸轮轮廓曲线进行后处理，最终得到实体凸轮模型。
    
    1在SolidWorks中建立凸轮机构装配关系
   
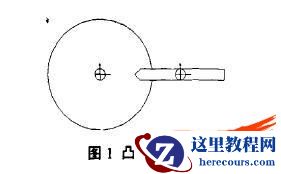
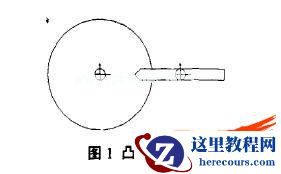
    在SolidWorks装配体界面建立如图1所示的装配关系，使凸轮的水平中心线和顶杆中心线重合，为构建准确的装配关系，精确定位凸轮和顶杆的接触点，顶杆的头部可设计成三角形。
   

    2设置约束和运动参数
   
    2．1添加约束
   
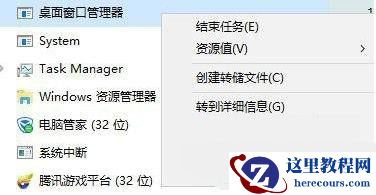
    在COSMOSMotion中构建运动模型时，不要按默认推荐情况设置约束和固定零件，应在部件属性设置栏把凸轮和顶杆都设为运动零件，如2图所示。在约束栏对装配体中的凸轮和顶杆分别添加旋转副和移动副约束，如图3所示。
   

    2．2设置运动参数
   
    凸轮为匀速转动；如表1所示顶杆往返运动的位移和时间关系不是函数关系，而是离散值。如引言所述，离散点凸轮轮廓曲线设计可通过用多项式等函数拟合各离散点，得到约束函数后再用函数式来驱动，但这样比较复杂，且会产生些累积误差。针对此类问题，COSMOS Motion可直接输入离散值，通过自带样条函数自动实现曲线拟合。如图4所示，在函数项选样条式，并在时间栏和位移栏分别按表1值手动输入，或用载入事先完成的txt或CSV格式的文件。