C++程序 针对由链表表示的两个数进行加法的-2

给定两个由链表表示的数字，编写一个函数返回它们的和。和列表是两个输入数字的加法的链表表示。不允许修改链表。同时，不允许使用显示的额外空间（提示：使用递归）。

示例：

输入：
第一个列表：5-〉6-〉3
第二个列表：8-〉4-〉2

输出：
结果列表：1-〉4-〉0-〉5

实践

我们已经在此处讨论了一种针对链表的解决方案，其中最不重要的数字是列表的第一个节点，而最重要的数字是最后一个节点。在这个问题中，最重要的节点是第一个节点，而最不重要的数字是最后一个节点，我们不能修改这些列表。这里使用递归从右到左计算总和。

以下是步骤：

计算给定的两个链表的大小。如果大小相同，则使用递归计算总和。在递归调用堆栈中保持所有节点直到最右边的节点，计算最右边节点的总和并向左侧转发进位。如果大小不同，则按以下步骤进行操作：

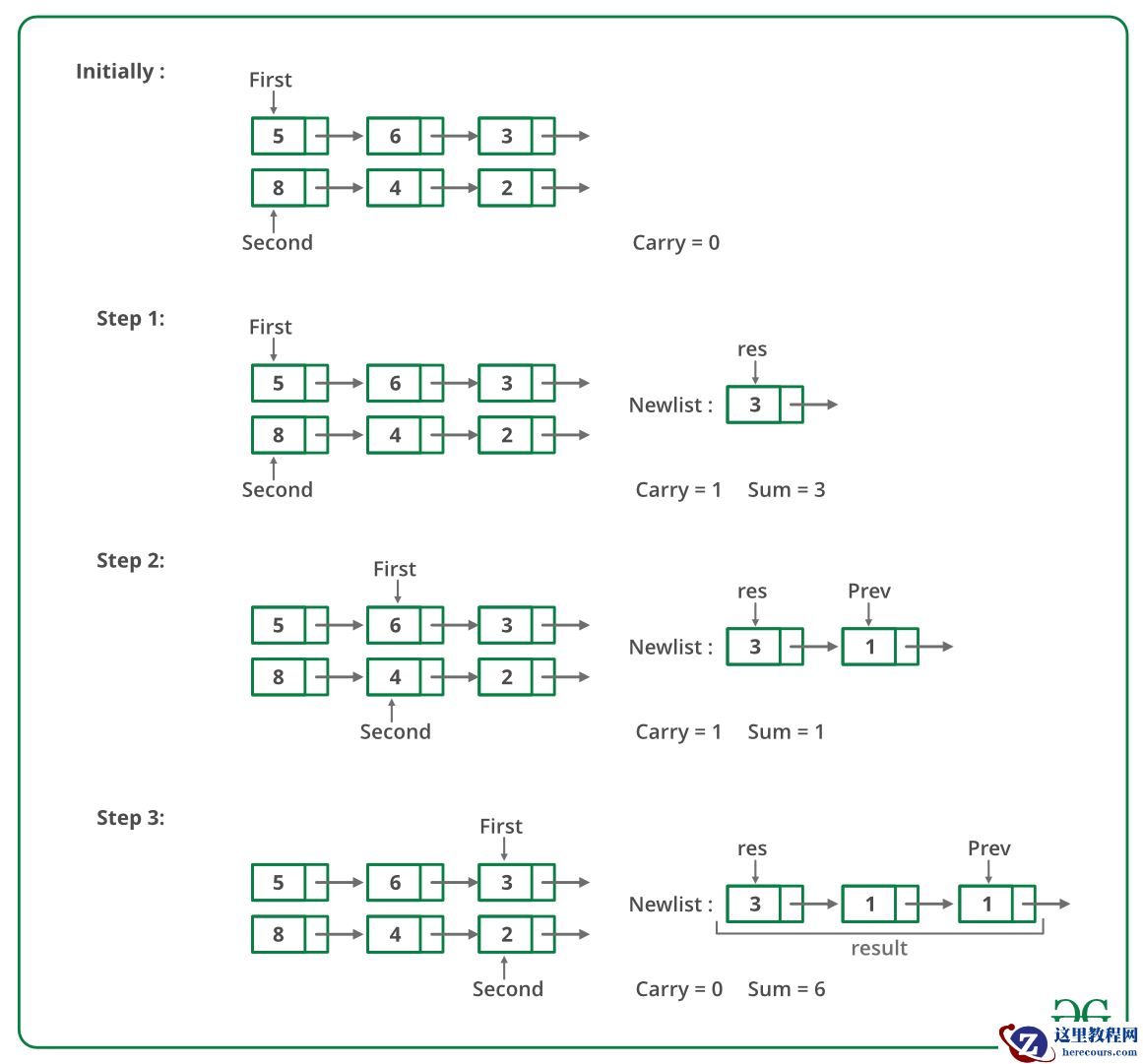
下面是上述方法的演示运行：

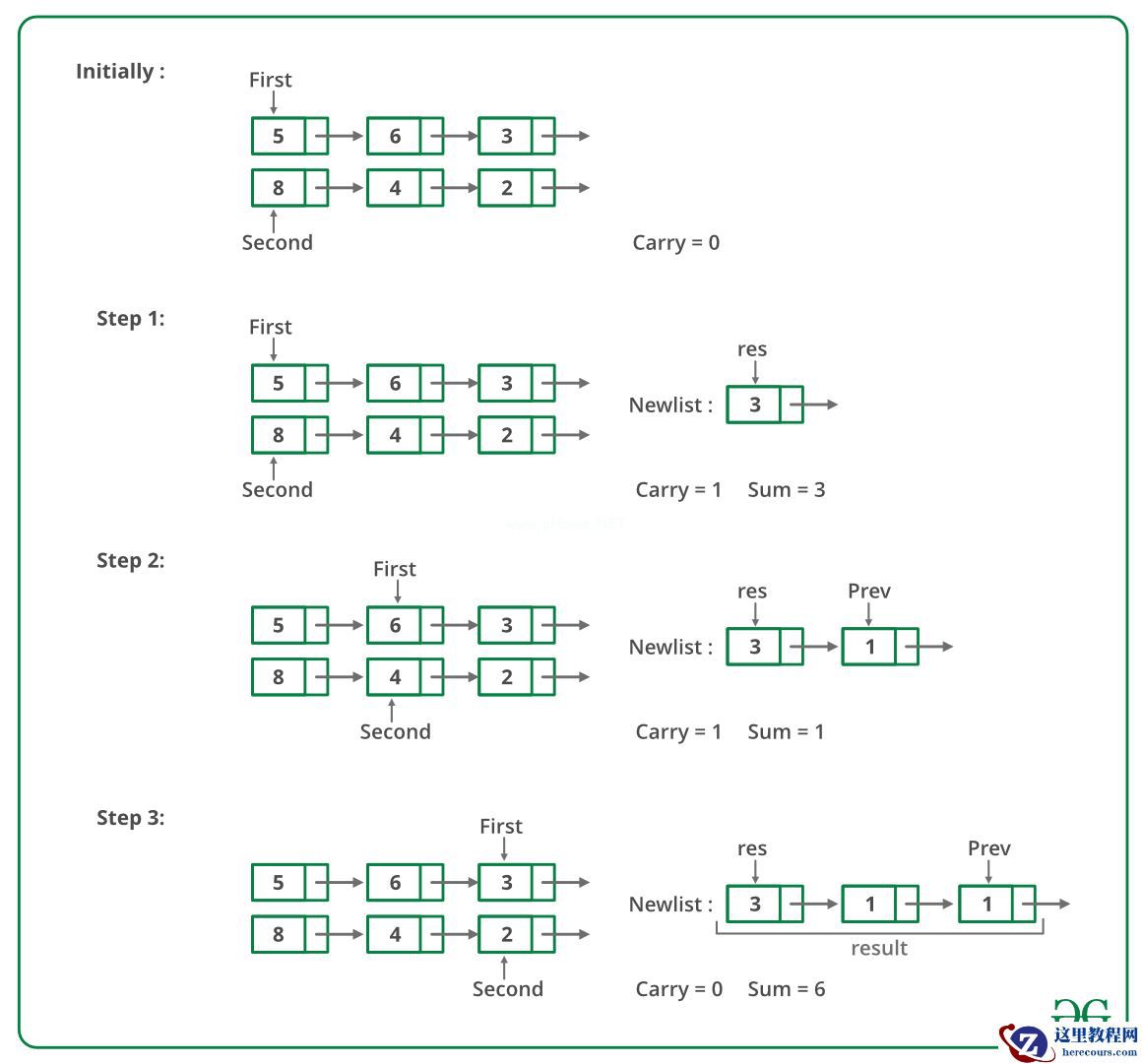
下面的图像实现了上述方法。

// C++递归程序，用于将两个链接列表相加#include <bits/stdc++.h>using namespace std;// 链接列表节点class Node{    public:    int data;    Node* next;};typedef Node node;/* 将节点插入到链接列表的开头 */void push(Node** head_ref, int new_data){    // 分配节点    Node* new_node = new Node[(sizeof(Node))];    // 写入数据    new_node->data = new_data;    // 将旧的列表与新的节点链接    new_node->next = (*head_ref);    // 将头移到新节点    (*head_ref) = new_node;}// 遍历和打印链接列表void printList(Node* node){    while (node != NULL)    {        cout << node->data << " ";        node = node->next;    }    cout << endl;}// 交换两个节点指针的函数void swapPointer(Node** a, Node** b){    node* t = *a;    *a = *b;    *b = t;}/* 计算链接列表的大小 */int getSize(Node* node){    int size = 0;    while (node != NULL)    {        node = node->next;        size++;    }    return size;}// 将相同大小的两个链接列表相加，分别由head1和head2表示，并返回结果的头部链接列表。当从递归返回时，进位被传播node* addSameSize(Node* head1, Node* head2, int* carry){    // 由于该函数假设链接列表的大小相同，因此检查任意两个头指针之一    if (head1 == NULL)        return NULL;    int sum;    // 分配内存给当前两个节点之和的节点    Node* result = new Node[(sizeof(Node))];    // 递归添加剩下的节点并取得进位    result->next = addSameSize(head1->next, head2->next, carry);    // 把当前两个数字和进位相加    sum = head1->data + head2->data + *carry;    *carry = sum / 10;    sum = sum % 10;    // 分配和给结果列表的当前节点    result->data = sum;    return result;}// 在较小的列表被添加到相同大小的大列表的子列表之后调用此函数。一旦右子列表被添加，就必须将进位加到较大列表的左边，以得到最终结果。void addCarryToRemaining(Node* head1, Node* cur, int* carry, Node** result){    int sum;    // 如果未遍历相同数量的节点，则加法进位    if (head1 != cur)    {        addCarryToRemaining(head1->next, cur, carry, result);        sum = head1->data + *carry;        *carry = sum / 10;        sum %= 10;        // 把这个节点添加到结果的最前面        push(result, sum);    }}// 添加由head1和head2表示的两个链接列表。两个列表的和存储在由result引用的列表中void addList(Node* head1, Node* head2, Node** result){    Node* cur;    // 第一个列表是空的    if (head1 == NULL)    {        *result =head2;        return;    }    // 第二个列表是空的    else if (head2 == NULL)    {        *result = head1;        return;    }    int size1 = getSize(head1);    int size2 = getSize(head2);    int carry = 0;    // 如果大小相等，则将相同大小的列表相加    if (size1 == size2)        *result = addSameSize(head1, head2, &carry);    else    {        int diff = abs(size1 - size2);        // 第一个列表应始终大于第二个列表。如果不是，则交换指针        if (size1 < size2)            swapPointer(&head1, &head2);        // 遍历大的列表，这个遍历从两个列表的剩余部分开始        for (cur = head1; diff--; cur = cur->next);        // 现在对于两个相同大小的列表，使用函数addSameSize()来做加法        *result = addSameSize(cur, head2, &carry);        // 使用现有大列表的引用，加上进位数字        addCarryToRemaining(head1, cur, &carry, result);    }    // 如果有进位，则将它附加到结果的第一个元素    if (carry)        push(result, carry);}// 主函数int main(){    Node *head1 = NULL, *head2 = NULL, *result = NULL;    int arr1[] = {9, 9, 9};    int arr2[] = {1, 8};    int size1 = sizeof(arr1) / sizeof(arr1[0]);    int size2 = sizeof(arr2) / sizeof(arr2[0]);    // 创建第一个链表    int i;    for (i = size1 - 1; i >= 0; --i)        push(&head1, arr1[i]);    // 创建第二个链表    for (i = size2 - 1; i >= 0; --i)        push(&head2, arr2[i]);    // 添加两个列表，并要求输出结果列表    addList(head1, head2, &result);    printList(result);    return 0;}

输出：

1 0 1 7

时间复杂度:

O(m+n)，其中m和n是给定两个链表的大小。

辅助空间 ：递归调用栈占用O(m+n)的空间

迭代方法：

此实现没有任何递归调用开销，因此是迭代解决方案。

由于我们需要从两个链表的最后开始添加数字，因此这里我们将使用栈数据结构来实现它。

// C++迭代程序添加两个// 链接列表 # include <bits/stdc++.h>using namespace std;   // 链接列表节点 class Node {     public:    int data;     Node* next; }; // 将新节点推入// 链接列表void push(Node** head_ref,          int new_data) {     // 分配节点    Node* new_node =          new Node[(sizeof(Node))];        // 放入数据    new_node->data = new_data;        // 将旧列表链接到    // 新节点    new_node->next = (*head_ref);        // 将头移动到指向    // 新节点    (*head_ref) = new_node; } // 添加两个新数字Node* addTwoNumList(Node* l1,                    Node* l2){    stack<int> s1,s2;    while(l1 != NULL)    {        s1.push(l1->data);        l1 = l1->next;    }    while(l2 != NULL)    {        s2.push(l2->data);        l2 = l2->next;    }    int carry = 0;    Node* result = NULL;    while(s1.empty() == false ||          s2.empty() == false)    {        int a = 0,b = 0;        if(s1.empty() == false)        {            a = s1.top();            s1.pop();        }        if(s2.empty() == false)        {            b = s2.top();            s2.pop();        }        int total = a + b + carry;        Node* temp = new Node();        temp->data = total % 10;        carry = total / 10;        if(result == NULL)        {            result = temp;        }        else        {            temp->next = result;            result = temp;        }    }    if(carry != 0)    {        Node* temp = new Node();        temp->data = carry;        temp->next = result;        result = temp;    }    return result;} // 打印链接列表void printList(Node *node) {     while (node != NULL)     {         cout << node->data << " ";         node = node->next;     }     cout < endl; } // 驱动程序int main() {     Node *head1 = NULL,         *head2 = NULL;        int arr1[] = {5, 6, 7};     int arr2[] = {1, 8};        int size1 = (sizeof(arr1) /                 sizeof(arr1[0]));     int size2 = (sizeof(arr2) /                 sizeof(arr2[0]));        // 创建第一个列表为5->6->7     int i;     for (i = size1-1; i >= 0; --i)         push(&head1, arr1[i]);        // 将第二个列表创建为1->8     for (i = size2-1; i >= 0; --i)         push(&head2, arr2[i]);          Node* result =          addTwoNumList(head1, head2);    printList(result);        return 0; }  

输出：

5 8 5

时间复杂度： O(m + n)，其中m和n是给定两个链表中节点的数量。

辅助空间： O(n)，其中n是栈中元素的数量