C++程序打印矩阵边界元素

来源：这里教程网时间：2026-02-16 16:08:25 作者：

C++程序打印矩阵边界元素

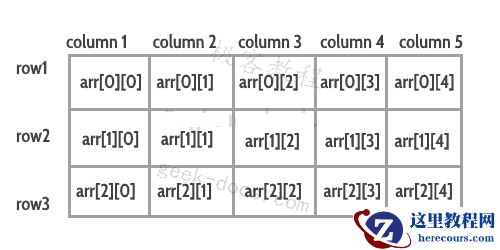
给定一个n x m的矩阵。打印矩阵的边界元素。边界元素是指不被四个方向的元素包围的元素，即第一行,第一列,最后一行和最后一列的元素。

示例:

输入:
1 2 3 4
5 6 7 8
1 2 3 4
5 6 7 8
输出:
1 2 3 4
5 8
1 4
5 6 7 8
说明: 打印了矩阵的边界元素。

输入:
1 2 3

5 6 7
1 2 3
输出:
1 2 3

5 7
1 2 3
说明: 打印了矩阵的边界元素。

方法: 思路很简单。遍历矩阵，检查每个元素是否位于边界上，如果是，则打印该元素，否则打印空格字符。

算法 :
从头到尾遍历数组。将外部循环指向行，内部循环遍历行中的元素。如果元素在矩阵的边界上，则打印该元素，即如果元素在第一行、第一列、最后一行或最后一列，则打印该元素。如果元素不是边界元素，则打印一个空格。
实现:

// C++ program to print boundary element // of matrix.#include <iostream>using namespace std;  const int MAX = 100;  void printBoundary(int a[][MAX], int m, int n){    for (int i = 0; i < m; i++)     {        for (int j = 0; j < n; j++)         {            if (i == 0 || j == 0 ||                 i == n - 1 || j == n - 1)                cout << a[i][j] << " ";            else                cout << " "                     << " ";        }        cout << endl;    }}  // Driver codeint main(){    int a[4][MAX] = {{1, 2, 3, 4},                      {5, 6, 7, 8},                      {1, 2, 3, 4},                      {5, 6, 7, 8}};    printBoundary(a, 4, 4);    return 0;}

输出:

1 2 3 4 5     8 1     4 5 6 7 8

复杂度分析:时间复杂度: O(n*n)，其中n为数组大小。这是通过矩阵的单次遍历实现的。空间复杂度: O(1)。因为只需要常量空间。

查找边界元素的总和

给定一个n x m的矩阵。找到矩阵的边界元素的总和。边界元素是指四个方向没有元素环绕的元素，即第一行,第一列,最后一行和最后一列的元素。

示例:

输入:
1 2 3 4

5 6 7 8
1 2 3 4
5 6 7 8
输出: 54
说明: 矩阵的边界元素
1 2 3 4
5 8
1 4
5 6 7 8
Sum = 1+2+3+4+5+8+1+4+5+6+7+8 =54
输入:
1 2 3

5 6 7
1 2 3
输出: 24
说明: 矩阵的边界元素
1 2 3

5 7
1 2 3

Sum = 1+2+3+5+7+1+2+3 = 24

方法： 此想法很简单。遍历矩阵，并检查每个元素是否位于边界上，如果是，则将它们相加以获取所有边界元素的总和。

算法：
创建一个变量来存储总和，并从开始到结束遍历数组。将外循环分配为指向行的指针，将内部循环遍历行的元素。如果元素位于矩阵的边界上，则将该元素添加到总和中，即如果元素位于第一行、第一列、最后一行、最后一列打印总和。
实现：

// C++程序查找矩阵的边界元素之和。

// C++ program to find sum of boundary elements// of matrix.#include <iostream>using namespace std;  const int MAX = 100;  int getBoundarySum(int a[][MAX],                    int m, int n){    long long int sum = 0;    for (int i = 0; i < m; i++)     {        for (int j = 0; j < n; j++)         {            if (i == 0)                sum += a[i][j];            else if (i == m - 1)                sum += a[i][j];            else if (j == 0)                sum += a[i][j];            else if (j == n - 1)                sum += a[i][j];        }    }    return sum;}  // Driver codeint main(){    int a[][MAX] = {{1, 2, 3, 4},                     {5, 6, 7, 8},                     {1, 2, 3, 4},                     {5, 6, 7, 8}};    long long int sum = getBoundarySum(a, 4, 4);    cout << "Sum of boundary elements is " <<              sum;    return 0;}

输出：